¶ Relations
This page contains a lot of duplications from the functions page..
Let be a relation from set into a set . Then the fact that is frequently written as .
¶ Relations between two sets
Let and be sets. A relation from into is any subset of .
The domain of is the set
The range of is the set
The inverse of is the relation from to defined as follows:
Now, in addition to , , and , consider a relation from to .
Then the composition of and is the relation from to defined as follows:
¶ Examples of relations between two sets
¶ Example
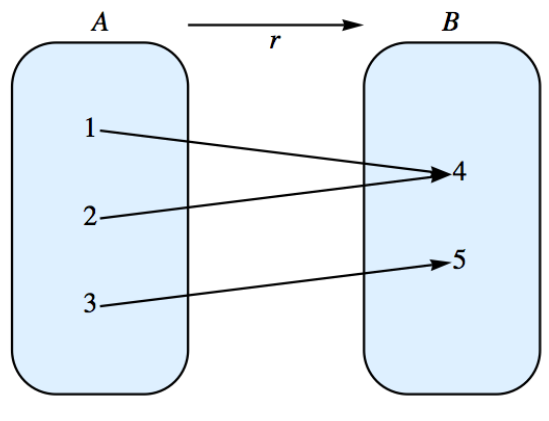
Let and . Then is a relation from into . There would be possible relations for these two sets.
A graph of this simple relation:
¶ Divisibility Example
Let and define a relation from into by iff . The set of pairs that qualify for membership is r=\
¶ Identity Relation Example
Suppose is a set. Let . Could also be defined by writing .
For example, if then .
¶ Relations on a set
A relation from a set into itself is called a relation on .
The "divides" relation, for example on the set of integers is: Let , . We say that divides , denoted by , iff there exists an integer such that .
¶ Composition of Relations
Let be a relation from a set into a set , and let be a relation from into a set . The composition of with , written (or ) , is the set of pairs of the form , where iff there exists such that and .
(Notice how we assumed that the second coordinates of pairs in and the first ocordinates of pairs in both come from . IF these sets were not the same, the composition would be undefined.
¶ Example
Take for example three sets
and two relations on those sets
so and .
Viewed graphically:
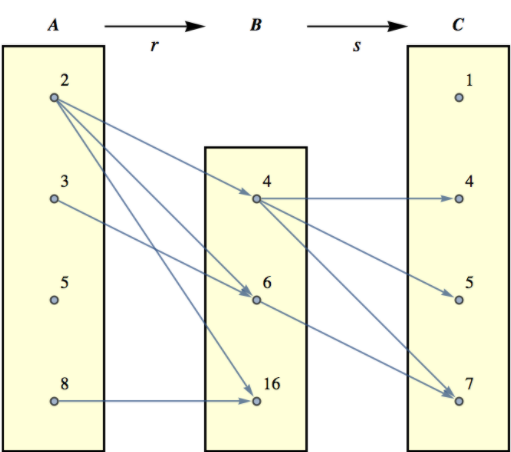
Note how certain elements in go through elements in to results in . That is,
Based on this, a new relation , from into can be defined. In order for to be in , it must be possible to travel along a path from to . In other words, iff and .
¶ Powers of a Relation
The powers of a relation can be recursively defined from the definition of a composite of two relations.
Let be a relation on the set . The powers , are defined recursively by
and so on.
¶ Example
Let . Find ,
¶ Solution
Because , we find that .
Because .
turns out to be the same as . It follows that for .
¶ Example 2
The relation on the set of real numbers is defined by
Find the composition of relations .
¶ Solution
By definition, the composition is the relation given by the following property:
where
To determine the composed relation , we solve the system of equations:
Hence, the composition is given by
It is clear that the composition is written in the form
¶ Graphs of Relations on a Set
In representing a relation as a graph, elements of are called the vertices (or node/point/junction) of the graph. They are typically represented by labeled points or small circles.We connect vertex to vertex with a narrow, called an edge (or arc, line, branch), going from vertex to vertex iff . This type of graph of a relation is called a directed graph or digraph.
¶ Example
Let and let .
and its digraph..
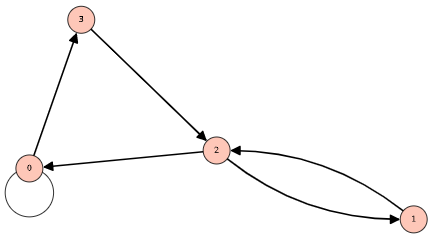
or
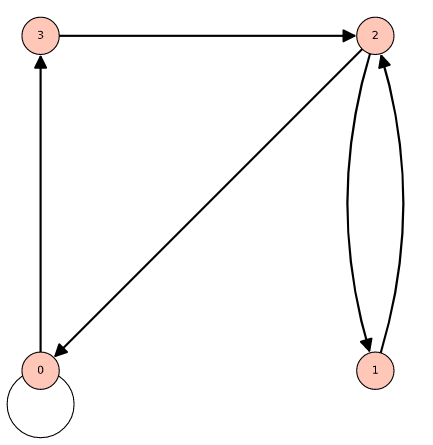
¶ Properties of Relations
¶ Individual Properties
¶ Reflexive
¶ Informal definition
Each element is related to itself.
¶ Formal Definition
Let be a set and let be a relation on . Then is reflexive iff for all .
Or
if for all
¶ Represented Graphically
Each point of the graph has an arrow looping from it and back onto itself.
¶ Irreflexive
¶ Informal definition
No element is related to itself.
¶ Formal definition
Let be a set and let be a relation on . Then is irreflexive iff for all .
Or
if for all
¶ Antisymmetric
¶ Informal definition
There are no pairs of distinct elements that are related to eachother. In other words, the only way for two elements to be related to eachother is for them to be the same element.
¶ Formal Definition
Let be a set and let be a relation on . Then is antisymmetric iff whenever and then is false.
Or
if for all
¶ Represented Graphically
Whenever there is an arrow going from one element to another distinct element, there is not an arrow going back from the second to the first.
¶ Transitive
¶ Informal definition
If any one element is related to a second and that second element is related to a third, then the first element is related to the third.
¶ Formal Definition
Let be a set and let be a relation on . is transitive iff whenever and then .
Or
if for all
¶ Represented Graphically
In each case where there is an arrow going from one point to a second and from the second point to a third, there is an arrow going form the first point to the third. That is, there are no "incomplete directed triangles" in the graph.
¶ Equivalence Relations
A relation on a set is called an equivalence relation iff it is reflexive, symmetric, and transitive.
¶ Symmetric
¶ Informal definition
If any one element is related to any other element, then the second element is related to the first.
¶ Formal Definition
Let be a relation on a set . is symmetric iff whenever , it follows that .
Or
if for all
¶ Represented Graphically
In each case where there is an arrow goign from one point to a second, there is an arrow going from the second point back to the first.
¶ Partial Orderings
A relation on a set that is reflexive, antisymmetric, and transitive is a partial ordering on set . A set on which there is a partial ordering relation is called a partially ordered set or poset.
¶ Partial Order by Function
We will define partial orders via the subset relation. For any element , we think of a function , such that is the set of properties that has. Then we relate different elements according to how their properites compare. All partial orders will arise this way.
For partial orders the symbols and are used because they resemble the symbols for subset and less-or-equal, which are the most common partial orders. (General orders are usually denoted by a letter like ).
¶ Formal Definition
Given any total function , from a set , to a collection of sets, define the binary relation on by the rule
for . A binary relation, , on a set, , is a partial order iff there is a such that agrees with for every pair of distinct elements. That is,
for all .
¶ Inverse Relations
Let be a relation from set to a set . The inverse relation from to , denoted by , is the set of ordered pairs .
For example, let and . Then the inverse of
If is any relation, then .
The domain and range of are equal to the domain and range of .
If is a relation on , then is also a relation on .
¶ Complementary Relations
Let be a relation from set to a set . The complementary relation is the set of ordered pairs .
¶ Combining Relations
Let be a relation from a set to a set and a relation from to a set .The composite of and is the relation consisting or ordered pairs where , , and for which there exists an element such that and . We denote the composite of and by .