A function assigns an element of one set, the domain, to elements of another set called the codomain.
The notation
indicates that is a function with domain and codomain .
The notation
indicates that assigns the element to . Here would be called the of at argument .
For example, consider two sets and a function. The first set is students in a discrete math class, . The second set are letter grades, . The function assigns letter grades to students. Suppose the grades assigned are for , for , for , for , for .
The domain of in the above example is the set of students. The codomain is the set of letter grades. The range of is the set since nobody is assigned a grade.
¶ Defining Functions
Every function can be described in four ways: algebraically (formula), numerically (a table), graphically, or in words.
Functions are often defined by formulas, for example . Notice how this won't assign a value for every element in the domain (value at 0 will be undefined).
Support of the function - The set of domain elements for which a function is defined.
Total function - A function that assigns a value to every element of its domain.
A function with a finite domain could be represented with a with a truth table to show the value of the function at each element of the domain. For example, a function where and are propositional variables is specified by:
¶ Image and Inverse Image
Given a function , the image (or range) of a function is the set of all output values it may produce. The image of set is the range of , which is the set of all possible images that can assume.
More formally, given a function , and , the image of under is defined as
In other words, is the set of all the images of the elements of .
Things to remember
- It is about the image of a subset 𝐶 of the domain of 𝐴 . Do not confuse it with the image of an element 𝑥 from 𝐴
- Therefore, do not merely say “the image.” Be specific: the image of an element, or the image of a subset.
- Better yet: include the notation 𝑓(𝑥) or 𝑓(𝐶) in the discussion.
- While 𝑓(𝑥) is an element in the codomain, 𝑓(𝐶) is a subset of the codomain.
- Perhaps, the most important thing to remember is:
If , then , and then there exists an such that .
¶ Examples
¶ Example 1
Let the function be defined by
We find the range of is We also have, for example, . It is clear that is neither one-to-one nor onto.
¶ Example 2
Let the function be defined by:
we find the range of is , and . The function is both one-to-one and onto.
¶ Example 3
Consider the function given by
Find and
¶ Solution
since and are the elements in the codomain to which sends 1 and 2.
since these are exactly the elements that sends to and .
since is not in the range of .
¶ Function Composition
Composing functions and means that is applied to some argument, , to produce , and then is applied to that result to produce .
For functions and , the composition , of with is defined to be the function from to defined by the rule:
for all .
¶ Types of Functions
(Diagrams of two example functions)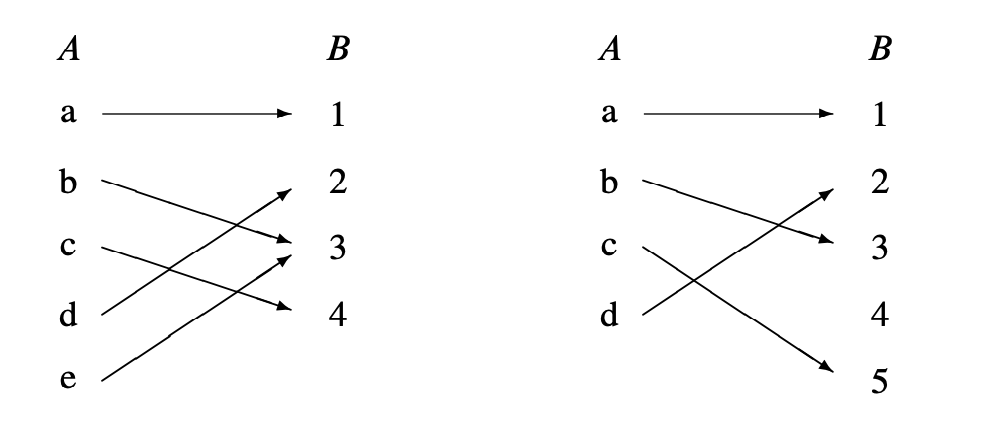
(Left is total and surjective, but not injective)
(Right is total and injective but not surjective)
(If is a function, it means that every point in the domain column, , has at most one arrow out of it. (If more than one arrow comes out of the first column, then it would be a relation not a function).
We say a function is:
¶ Total and Partial
Total if every element of is assigned to some element of , otherwise is called a partial function.
" is total" means that every point in the domain column of a function graph has at least one arrow out of it, which really means it has exactly one arrow out of it since is a function.
¶ Surjective
If every element of is mapped at least once. Also known as onto.
This is a property of the codomain.
For every element , there exists an element such that
" is surjective" means that every point in the codomain column has at least one arrow into it.
If is a finite set, we let be the number of elements in . If is surjective, then .
¶ Injective
If every element of is mapped to at most once. Also known as one-to-one. This is a property of the domain of a function.
" is injective" means that every point in the codomain column, , has at most one arrow into it.
If is a finite set, we let be the number of elements in . If is total and injective, then .
for all elements
¶ Bijective
If is total, surjective, and injective. In particular, each element of is mapped to exactly once.
" is bijective" means that every point in the column has exactly one arrow out of it, and every point in the column has exactly one arrow into it.
If is a finite set, we let be the number of elements in . If is bijective, then .
¶ Increasing and Decreasing
A function whose domain and codomain are subsets of the set of real numbers is increasing if and strictly increasing if , wherever and and are in the domain of . is decreasing if and stricly decreasing if
¶ Equivalence Relations
¶ Equivalence by Function
Given any total function with domain , define the binary relation on by the rule
for all
A binary relation is an equivalence relation iff it equals for some .
Abstractly, we assume there is some function that extracts the angles, size, color, or whatever other property of elements we’re interested in. Two elements would be considered equivalent iff the function extracts the same value for each.
For example, if is the function mapping a triangle to the lengths of its sides, then determines the congruence relation. If is the function mapping a triangle to the sizes of its angles, then determines the similarity relation.
¶ Partitions
A partition of a set , is a collection , of nonempty sets called the blocks of the partition such that
- and
- if are blocks of , then and are disjoint (they have no elements in common and their intersection is empty).
For example, we can partition the integers into four blocks according to whether their remainder on division by is , , , or :
We could partition the pixels of an image by their color. So there will be between and several million blocks depending on whether the image is pure black and white or is true color.
The relation of being in the same block is an equivalence relation. We can extract an equivalence relation from any partition, and conversely, we can define a partition determined by any equivalence relation. Partitions and equivalence relations are interchangeable ways of talking about the same thing.
¶ Properties of Equivalence Relations
¶ Reflexive
for every element .
A relation on a set is reflexive iff for every , .
In a reflexive relation, an element is always related to itself. For example, let be the relation on the set of all people consisting of pairs where and have the same mother and the same father. Then for every person .
¶ Irreflexive
A relation on the set is irreflexive if for every , . That is, is irreflexive if no element in is related to itself.
¶ Symmetric
whenever , for all .
A relation on is symmetric iff for all , if then .
In other words, a relation is symmetric iff is related to always implies that is related to .
The equality relation is symmetric since .
¶ Asymmetric
A relation is called asymmetric if implies that .
¶ Antisymmetric
A relation on a set such that for all , if and , then is called antisymmetric.
In other words, a relation is antisymmetric iff there are no pairs of distinct elements and with related to and related to .That is, the only way to have related to and related to is for and to be the same element.
In terms of arrow diagrams of a relation, saying that a relation is antisymmetric is the same as saying that whenever there is an arrow going from one one element to another distinct element, there is not an arrow going back from the second to the first.
The less than or equal to relation is antisymmetric. and implies .
Note that symmetric and asymmetric are not opposites. A relation can have both or lack both.
¶ Transitive
A relation on a set is called transitive if whenever and , then , for all
For example, by . Since and then is true for all , then is transitive.
¶ Equivalence Classes
Let be an equivalence relation on a set . The set of all elements that are related to an element of is called the equivalence class of . The equivalence class of with respect to is denoted by . When only one relation is under consideration, we can delete the subscript and write $\lbrack a \rbrack $ for this equivalence class.
¶ Combining Relations
Relations from to are subsets of , two relations from to can be combined in any way two sets can be combined.
Let be a relation from set to set and a relation from to a set . The composite of and is the relation consisting of ordered pairs where and , and forwhich there exists an element such that and . We denote the composite of and by
¶ Examples
(Some examples below use the following relations..)
, the "greater than" relation,
, the "greater than or equal to" relation,
, the "less than" relation,
, the "less than or equal to" relation,
, the "equal to" relation,
, the "unequal to"relation.
¶ Example
all of . It's always true that or , so the relation always holds.
. contains when or . This only happens when ,
. contains when , which happens preciesly when .
contains when , which is also true for .
, which is equivalent to It is impossible for both and to hold at the same time, so the answer is .
since we want , which is
.
¶ Example
Consider and . The relations and can be combined to obtain
¶ Partial Orders
A relation on a set is called a partial ordering if it is antisymmetric and transitive. A set together with a partial ordering is called a partially ordered set, or poset, and is denoted by Members of set are called elements of the poset.
A general example of a partial order is the subset relation on sets. For any element, , we think of a function, , such that is the set of properties that has. Then we relate different elements according to how their properties compare.
For partial orders the symbols or (or ) are used because they resemble the symbols used for subset and less-or-equal, which are the most common partial orders.
A partial order is called weak iff it is reflexive.
A partial orer is called strict iff it is irreflexive.
The most familiar examples of partial orders are the "less than relations", for example, the relation on real numbers. To see that is indeed a partial order, just define . Since there is a rational number between any two real numbers, it follows that is simply . Likewise, the relation is a partial order because it agrees with for all pairs of distinct real numbers.
¶ Definitions
Given any total function, , form a set, , to a collection of sets, define the binary relation on by the rule
for . A binary relation, , on a set, , is a partial order if and only if ther eis a such that agrees with for every pair of distinct elements. That is,
for all
A partial order is called weak iff it is reflexive. For example, the relation on the real numbers and the relation on sets, are weak partial orders.
A binary relation, , on a set, , is irreflexive iff for all it is not true that . A partial order is strict iff it is irreflexive.
The relation on the reals and the proper subset relation are strict partial orers. In general, a partial order may be neither weak nor strict; this happens when some elements are related to themselves and others are not.
¶ Properties of Partial Orders
Every partial order is transitive.
A binary relation, , on a set, , is antisymmetric if
for all
Every partial order is antisymmetric.
¶ Total Orders
Given any two numbers, one will be bigger than the other. Partial orders with this property are total orders.
Let be a binary relation on a set, , and let be elements of . Then and are comparable with respect to iff ( or ). A partial order under which every two distinct elements are comparable is called a total order.
¶ Products of Relations
The product, , of relations and is defined to be the relation with
Products preserve several of the relation properties we have considered. Transitivity, symmetry, reflexivity, and antisymmetry are preserved for if both and have those properties.
Products dont preserve the property of being a total order. In the below example relating to age and height pairs, and are incomparable under so is not total even though both and are.
¶ Example of Product of Relations
Define relation on age-heght pairs of being younger and shorter. This is the relation on the set of pairs where is a nat num (age in months) and is a natural number describing height in inches. is defined by the rule
¶ Restrictions of Relations
Let be a relation of set , and let be a subset of . The restriction of to is the relation on whose graph is
Restriction preserves transitivity, symmetry, antisymmetry, asymmetry, refexivity, and irreflexivity. It doesn't preserve everything though (like surjectivity, nor whether it is a total relation).