A set is a bunch of objects, which are called elements of the set.
N = { 0 , 1 , 2 , 3 , … } the natural numbers C = { red, blue, yellow } primary colors D = { Teddy, Sheba, Bella } dead pets P = { { a , b } , { a , c } , { b , c } } a set of sets N C D P = { 0 , 1 , 2 , 3 , … } = { red, blue, yellow } = { Teddy, Sheba, Bella } = { { a , b } , { a , c } , { b , c } } the natural numbers primary colors dead pets a set of sets
The order of elements in a set don't matter.
Any object only appears in a set once (it's either in the set or not).
The expression e ∈ S e ∈ S e e S S
symbol set elements ∅ the empty set none N nonnegative integers { 0 , 1 , 2 , 3 , … } Z integers { … , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , … } Q rational numbers 1 2 , − 5 3 , 16 , etc. R real numbers π , e , − 9 , 2 , etc. C complex numbers i , 19 2 , 2 − 2 i , etc. symbol ∅ N Z Q R C set the empty set nonnegative integers integers rational numbers real numbers complex numbers elements none { 0 , 1 , 2 , 3 , … } { … , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , … } 2 1 , − 3 5 , 1 6 , etc. π , e , − 9 , 2 , etc. i , 2 1 9 , 2 − 2 i , etc.
A superscript + or - restricts a set to positive or negative elements.
¶ Comparing and Combining Sets
X ⊆ Y X ⊆ Y X X Y Y X X Y Y
X ⊂ Y X ⊂ Y X X Y Y
X ⊆ Y ↔ ( x ∈ X ⟶ x ∈ Y ) X ⊆ Y ↔ ( x ∈ X ⟶ x ∈ Y )
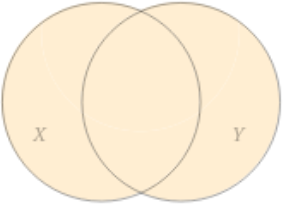
X ∪ Y X ∪ Y X X Y Y X X Y Y
x ∈ X ∪ Y ↔ x ∈ X ∨ x ∈ Y x ∈ X ∪ Y ↔ x ∈ X ∨ x ∈ Y
X ∪ Y = { x ∣ x ∈ X or x ∈ Y } X ∪ Y = { x ∣ x ∈ X or x ∈ Y }
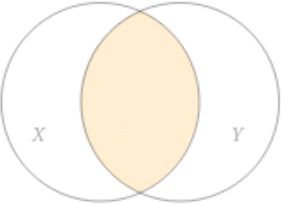
X ∩ Y X ∩ Y X X Y Y X X Y Y
x ∈ X ∩ Y ↔ x ∈ X ∧ x ∈ Y x ∈ X ∩ Y ↔ x ∈ X ∧ x ∈ Y
X ∩ Y = { x ∣ x ∈ X and x ∈ Y } X ∩ Y = { x ∣ x ∈ X and x ∈ Y }
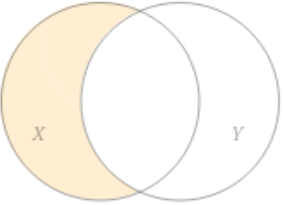
X − Y X − Y X \ Y X \ Y X X Y Y X X Y Y
x ∈ X − Y ↔ x ∈ X ∧ x ∉ Y x ∈ X − Y ↔ x ∈ X ∧ x ∈ / Y
X − Y = { x ∣ x ∈ X and x ∉ Y } X − Y = { x ∣ x ∈ X and x ∈ / Y }
(not clear if ⊕ ⊕ ⊕ ⊕ XOR XOR
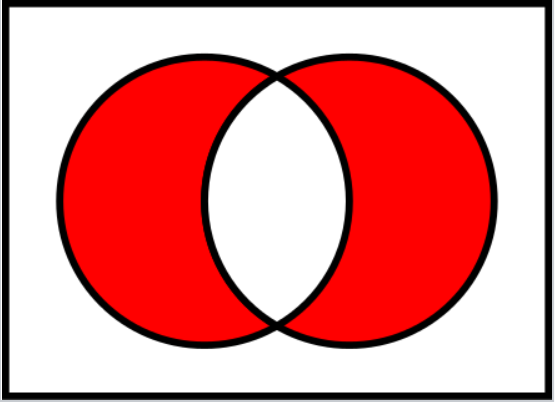
X ⊕ Y X ⊕ Y X ⊖ Y X ⊖ Y X △ Y X △ Y X X Y Y X X Y Y
x ∈ X ⊕ Y ≡ x ∈ X ≢ x ∈ Y x ∈ X ⊕ Y ≡ x ∈ X ≡ x ∈ Y
X ⊕ Y = ( X − Y ) ∪ ( Y − X ) X ⊕ Y = ( X − Y ) ∪ ( Y − X )
X × Y X × Y X X Y Y
X × Y = { ( x , y ) ∣ x ∈ X ∧ y ∈ Y } X × Y = { ( x , y ) ∣ x ∈ X ∧ y ∈ Y }
The notation X 2 X 2 X × X X × X X 3 X 3 X × X × X X × X × X
X n = { ( x 1 , x 2 , … , x n ) ∣ x i ∈ X for i = 1 , 2 , … , n } X n = { ( x 1 , x 2 , … , x n ) ∣ x i ∈ X for i = 1 , 2 , … , n }
The cartesian product X × Y X × Y x y x y
Often all the sets being considered are subsets of a known domain of discourse D D A A D D A ˉ A ˉ D D not in A A A ˉ : : = D − A A ˉ : : = D − A A ˉ A ˉ A A
For example, the complement of positive real numbers is the set of negative real numbers together with zero when the domain is all real numbers.
R + ‾ = R − ∪ { 0 } R + = R − ∪ { 0 }
If A A U U A A
A ˉ = { x ∈ U ∣ x ∉ A } A ˉ = { x ∈ U ∣ x ∈ / A }
The collection of all subsets of a set. If A A n n 2 n 2 n p o w ( A ) p o w ( A )
B ∈ pow ( A ) IFF B ⊆ A B ∈ p o w ( A ) IFF B ⊆ A
If A A B B f : A → B f : A → B B B P ( A ) P ( A ) f f A A A A
The power set of the empty set ∅ ∅ 2 0 = 1 2 0 = 1
Used to describe sets that cannot be listed by elements or taking unions, intersections, etc.
The idea is to define a set using a predicate . The set consists of all values that make the predicate true.
A = { n ∈ N ∣ n is a prime and n = 4 k + 1 for some integer k } A = { n ∈ N ∣ n is a prime and n = 4 k + 1 for some integer k }
The set A A n n
" n is a prime and n = 4 k + 1 for some integer k ′ ′ " n is a prime and n = 4 k + 1 for some integer k ′ ′
is true. The smallest elements of A A
5 , 13 , 17 , 29 , 37 , 41 , 53 , 57 , 61 , 73 , … 5 , 1 3 , 1 7 , 2 9 , 3 7 , 4 1 , 5 3 , 5 7 , 6 1 , 7 3 , …
B = { x ∈ R ∣ x 3 − 3 x + 1 > 0 } B = { x ∈ R ∣ x 3 − 3 x + 1 > 0 }
The set B B x x
x 3 − 3 x + 1 > 0 x 3 − 3 x + 1 > 0
is true.
C = { a + b i ∈ C ∣ a 2 + 2 b 2 ≤ 1 } C = { a + b i ∈ C ∣ a 2 + 2 b 2 ≤ 1 }
Set C C a + b i a + b i
a 2 + 2 b 2 ≤ 1 a 2 + 2 b 2 ≤ 1
Two sets are equal if they have exactly the same elements. X = Y X = Y z ∈ X z ∈ X z ∈ Y z ∈ Y z z
Theorem: Let A A B B C C
A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )
Note: above read as "The intersection of set A with the union of set B and set C is equivalent to the union of the intersections of sets A and B and sets A and C"
Proof: The equality is equivalent to the assertion that
x ∈ A ∩ ( B ∪ C ) ⟺ x ∈ ( A ∩ B ) ∪ ( A ∩ C ) x ∈ A ∩ ( B ∪ C ) ⟺ x ∈ ( A ∩ B ) ∪ ( A ∩ C )
for all x. We prove the above assertion by using a chain of iff's.
Definition of intersection:
x ∈ A ∩ ( B ∪ C ) ⟺ ( x ∈ A ) ∧ ( x ∈ B ∪ C ) x ∈ A ∩ ( B ∪ C ) ⟺ ( x ∈ A ) ∧ ( x ∈ B ∪ C )
Definition of union:
( x ∈ A ) ∧ ( x ∈ B ∪ C ) ⟺ ( x ∈ A ) ∧ ( x ∈ B ∨ x ∈ C ) ( x ∈ A ) ∧ ( x ∈ B ∪ C ) ⟺ ( x ∈ A ) ∧ ( x ∈ B ∨ x ∈ C )
AND distributivity:
( x ∈ A ) ∧ ( x ∈ B ∨ x ∈ C ) ⟺ ( x ∈ A ∧ x ∈ B ) ∨ ( x ∈ A ∧ x ∈ C ) ( x ∈ A ) ∧ ( x ∈ B ∨ x ∈ C ) ⟺ ( x ∈ A ∧ x ∈ B ) ∨ ( x ∈ A ∧ x ∈ C )
Definition of intersection
( x ∈ A ∧ x ∈ B ) ∨ ( x ∈ A ∧ x ∈ C ) ⟺ ( x ∈ A ∩ B ) ∨ ( x ∈ A ∩ C ) ( x ∈ A ∧ x ∈ B ) ∨ ( x ∈ A ∧ x ∈ C ) ⟺ ( x ∈ A ∩ B ) ∨ ( x ∈ A ∩ C )
Definition of union
( x ∈ A ∩ B ) ∨ ( x ∈ A ∩ C ) ⟺ x ∈ ( A ∩ B ) ∪ ( A ∩ C ) ( x ∈ A ∩ B ) ∨ ( x ∈ A ∩ C ) ⟺ x ∈ ( A ∩ B ) ∪ ( A ∩ C )
■ ■