¶ Power Functions
Let be any nonnegative real number. Define , the power function with exponent , as follows:
for each nonnegative real number .
¶ Floor Functions
¶ Graph of a Multiple of a Function
A multiple of a function is obtained by multiplying every value of the function by a fixed number. To understand the concept of -notation, it is helpful to understand the relation between the graph of a function and the graph of a multiple of the function.
Let be a real-valued function of a real variable and let be any real number. The function , called the multiple of by or times , is the real-valued function with the same domain as that is defined by the rule
¶ Increasing and Decreasing Functions
Consider the absolute value function, , defined as follows:
When , the graph of is the same as the graph of , the straight line with slope 1 that passes through the origin . For , the graph of is the same as the graph of , which is the straight line with slope that passes through (See below graph of absolute value function)
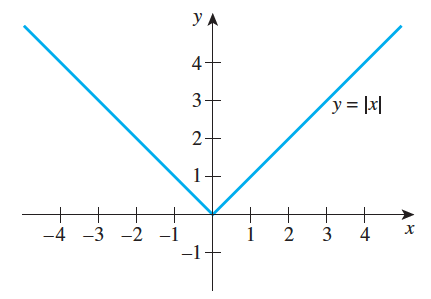
Note that as you trace from left to right along the graph to the left of the origin, the height of the graph continually decreases. For this reason, the absolute value function is said to be decreasing on the set of real numbers less than . On the other hand, as you trace from left to right along the graph to the right of the origin, the height of the graph continually increases. Consequently, the absolute value function is said to be increasing on the set of real numbers greater than .
¶ Definition
Let be a real-valued function defined on a set of real numbers, and suppose the domain of contains a set . We say that is increasing on the set if, and only if,
for all real numbers and in , if then .
We say that is decreasing on the set if, and only if,
for all real numbers and in , if then .
We say that is an increasing (or decreasing) function if, and only if, is increasing (or decreasing) on its entire domain.