¶ Propositional Logic
¶ Propositions
A statement that is either true or false.
A proposition is atomic if it cannot be broken down into smaller statements / propositions. Otherwise, it is called molecular.
¶ Logical Connectives
is read "P or Q"
is read "P and Q"
is read "if P then Q"
is read "P if and only if Q"
is read "not P"
Note that the OR is the inclusive or and that is true when both P and Q are true.
¶ Truth Conditions for Connectives
is true when P or Q or both are true
is true when both P and Q are true
is true when P is false or Q is true or both
is true when P and Q are both true, or both false.
is true when P is false.
¶ Negation
Note that the notation for negation isn't standardized. and are the most common, you might also see , , , , and
The negation of the English sentence "Bob’s smartphone has at least 32 GB of memory” is “Bob’s smartphone does not have at least 32 GB of memory”. This could be rewritten more simply as "Bob's cellphone has less than 32 GB of memory."
Note how in this specific case, "greater than or equal to 32 GB" becomes "less than 32GB" so we go from to
¶ Implications
"if P then Q". Often rephrased as .
P is the hypothesis (or antecedent)
Q is the conclusion (or consequent)
An implication is true provided P is false or Q is true (or both), and false otherwise. In particular, the only way for P → Q to be false is for P to be true and Q to be false.
- Quadratic Formula - If .
¶ Converse Inverse, and Contrapositive
The converse of an implication is the implication . An example of a true implication and a false converse woul be, "If a shape is a square, then it is a rectangle". Or, "If a number greater than 2 is prime, then that number is odd" (Just because a number is odd does not mean it is prime).
There can be implications that's converse is also true. For example, the pythagorean theorem has a true converse. Is , then the triangle with sides a, b, and c is a right triangle.
The contrapositive of an implication is the statement . An implication and its contrapositive are logically equivalent. The contrapositive can be helpful in deciding whether an implication is true: often it is easier to analyze the contrapositive.
If an implication and its converse are true, we say that P and Q are equivalent and write ( the biconditional).
The inverse of a proposition is
¶ If and only if
is logically equivalent to .
Example: Given an integer , it is true that is even if and only if is even. That is, if is even, then is even, as well as the converse: if is even, then is even.
¶ Proof Method #1
In order to prove :
- Write, "Assume P".
- Show that Q logically follows.
¶ Example 1 of Proof Method #1
Theorem:
Scratchwork: We can factor to get .For between 0 and 2, all the terms on the right side are nonnegative. We can organize our observations into a formal proof.
Proof: Assume . Then, , , and are all nonnegative. Therefore, the product of these terms is also nonnegative. Adding 1 to this product gives a positive number, so:
Multiplying out on the left side proves that
as claimed.
Note: Proofs typically begin with the word "Proof" and end with some sort of delimiter like , , or "QED".
¶ Example 2 of Method #1
Theorem: If two numbers and are even, then their sum is even.
Proof: Assume the numbers and are even. This means that and for some integers and . The sum is then . Since is an integer, this means that is even.
Notice we just assume P is true and repeatedly ask and answer the question, "What does that mean?". Eventually we conclude that it means the conclusion.
¶ Logic and Bit Operations
Computer bit operations correspond to the logical connectives.
Below is a table for the bit operators OR ()
¶ Applications of Propositional Logic
Propositional logic and its rules can be used to design computer circuits, to construct computer programs, to verify the correctness of those programs, and to solve many familiar puzzles. Software systems based on the rules of logic have been developed for constructing some, but not all, types of proofs automatically
¶ Translating English Sentences
“You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old., where
"You can ride the roller coaster"
"You are under 4 feet tall"
"You are older than 16 years old"
(There are other ways to represent this sentence)
¶ Boolean Searches
¶ Logic Puzzles
¶ Logic Circuits
¶ Propositional Equivalences
A compound proposition that is always true, no matter the truth values of the propositional variables that occur in it, is a tautology. A compound proposition that is always false is a contradiction.
¶ De Morgans Laws
De Morgan's laws for negating conjunctions and disjunctions.
¶ Conditional-Disjunction Equivalence
and are logically equivalent.
¶ Constructing New Logical Equivalences
Below, we show that and are logically equivalent.
Another example, we show that and are logically equivalent by developing a series of logical equivalences.
¶ Satisfiability
A compound proposition is satisfiable if there exists an assignment of truth values to its variables that makes it true (when its a tautology or contingency).
When a compound proposition is false for all assignments of truth values to its variables, it is unsatisfiable.
is an example of unsatisfiable. For it to be true, both and must both be true. But for the former, all three variables must have the same truth variable and for the latter at least one must be true and one must be false. This is a contradiction, so we can conclude that there does not exist an assignment of truth variables that makes the compound proposition true.
¶ Applications of Satisfiability
Many problems in diverse areas such as robotics, software testing, artificial intelligence planning, computer-aided design, machine vision, integrated circuit design, scheduling, computer networking, and genetics, can be modeled in terms of propositional satisfiability.
¶ Examples of Applications of Satisfiability
¶ n Queens Problem
The queens problem asks for a placement of queens on an chessboard so that no queen can attack another queen. This means that no two queens can be placed in the same row, column, or diagonal to one another.
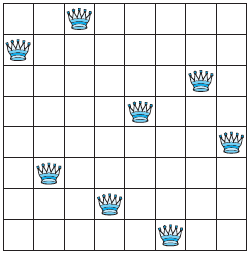
(th row th column, starting from top left square)
To model this as a satisfiability problem, we introduce variables for and . For a given placement of a queens on the chessboard, is true when there is a queen on the square in the row and column, and is false otherwise.
Note that squares and are on the same diagonal if either or . Note in the picture above of our chessboard, and are true, and and are false.
For no two of the queens to be in the same row, there must be one queen in each row. We can show that there is one queen in each row by verifying that every row contains at least one queen and that every row contains at most one queen.
We note that asserts that row contains at least one queen, and
asserts that every row contains at least one queen.
For every row to include at most one queen, it must be the case that and are not both true for integers and with . Observe that asserts that at least one of and is true, which means that at least one of and is false. So to check that there is at most one queen in each row, we assert
To assert that no column contains more than one queen, we assert that
(This assertion, together with the previous assertion that every row contains a queen, implies that every column contains a queen.)
To assert that no diagonal contains two queens, we assert
and
The innermost conjunction in and in for a pair runs through the positions on a diagonal that begin at and runs rightward along this diagonal. The upper limits on these innermost conjunctions identify the last cell in the board on each diagonal.
Putting this all together, the solution to the queens problem are the assignments of truth values to the variables for and that make
true.
So to recap:
is a conjunction of disjunctions which require for every row there is at least one queen.
The rest of the constraints are forbidding pairs of queens from being placed at certain locations.
is forbidding placing two queens in the same row. That is, we for forbid for any , , and .
is to forbid placing two queens in the same column. This condition for .
and are to forbid placing two queens in the same forward and backward diagonal respectively.
¶ Sudoku
Sudoku is a number puzzle that consists of a grid for any positive integer , with the grid made up of subgrids. Some of the cells in the grid are assigned one of the numbers
and all the other cells are blank. The puzzle is solved by assigning a number to each blank cell so that every row, column, and subgrids contains each of the numbers.
To encode sudoku as a constraint satisfaction problem, we let denote the proposition that is true when number is in the th row and th column.
Then we construct the following compound propositions:
- Every row contains every number
- Every column contains every number
- Every block contains every number
- Each cell contains no more than 1 number
(We take the conjunction over all valeus of , , , and , where each variable ranges from to and of
The puzzle is solved by finding an assigment of truth values for each of the proposition that make the conjunction of our compound propositions true.
For for example (a grid, the most common sudoku configuration), there are such propositions.
To construct the assertion that every row contains every number (in this case, ):
- Assert that row contains the number
- Assert row contains all numbers, we form the conjunction of the above disjunctions over all possible values of .
- Finally, to assert every row contains every number, we take the conjunction of over all nine rows. This gives us
¶ Simplifying Statement Forms
Use the different forms of logical equivalences to replace sections of a statement. Keep making replacements until the proposition we start with is the one we want to compare equality of.
¶ Examples
¶ Example 1
Verify the logical equivalence