¶ Problems 1
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 1
A real number r is called sensible if there exist positive integers and such
that . For example, setting and shows that is sensible. Prove that is not sensible. (Consider only positive real roots in this problem).
¶ Solution
We use proof by contradiction. Suppose that where a and b are two positive integers.
We cube both sides to get .
We divide both sides to get . This implies a is an even integer. If is an even integer, that means that is an even integer as well.
We can rewrite as for some unknown integer . Therefore,
We see that b is also even (its a multiple of 4). Since a and b are both even, they are not coprime numbers, which is a contradiction.
Since we have a contradiction, we must assume that is irrational.
¶ Problem 1 (From In-Class Problems MIT OCW 6.042J Spring '15)
The Pythagorean Theorem says that if a and b are the lengths of the sides of a right triangle, and c is the length of its hypotenuse, then
In this problem we'll examine a particularly simple “proof without words” of the theorem.
Suppose you are given four different colored copies of a right triangle with sides of lengths a, b and c, along with a suitably sized square, shown below.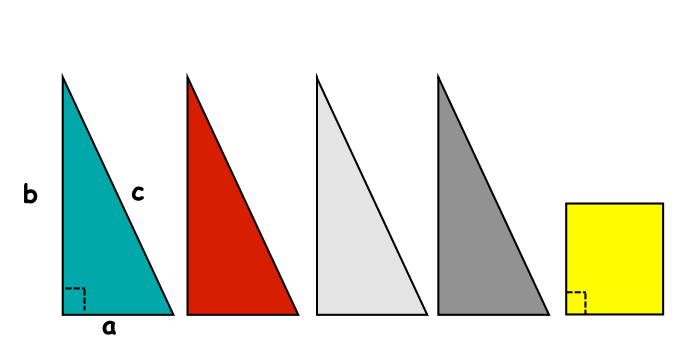
(a) You will first arrange the square and four triangles so they form a square. From this arrangement you will see that the square is
(b) You will then arrange the same shapes so they form two squares, one and the other .
You know that he area of an square is . Appealing to the principle that area is preserved by rearranging, we can conclude that as claimed.
One concern is that there might be something special about the shape of these particular triangles and squares that makes the rearranging possible - for exmaple, suppose .
(c) How would you respond to this concern?
(d) Another concern is that a number of facts about right triangles, squares and lines are being implicitly assumed in justifying the rearrangements into squares. Enumerate some of these assumed facts.
¶ Solution (WIP)
a) 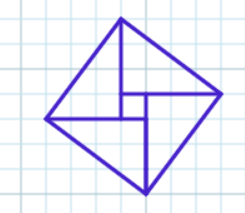
We see that that the square is .
b)
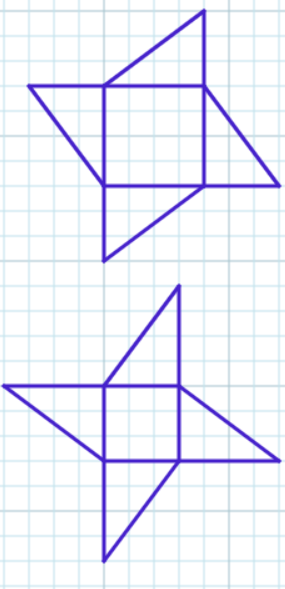
Triangles rearranged to form bxb square and a cxc square.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 2
Translate the following sentence into a predicate formula:
There is a student who has emailed exactly two other people in the class, besides possibly herself.
The domain of discourse should be the set of students in the class; in addition, the only predicates that you may use are equality and E(x, y), meaning that “x has sent email to y.”
¶ Solution
The above is translated to: "There exists students , , and where send an email to AND sent an email to AND is not the same as AND is not the same as and is not the same as AND for all students , x sent an email to a student s where the student s is x OR the student s is y OR the student s is z.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 3
Express each of the following predicates and propositions in formal logic notation. The domain of discourse is the nonnegative integers,
In addition to the propositional operators, variables and quantifiers, you may define predicates using addition, multiplication, and equality symbols, but no constants (like 0, 1, . . .). For example, the proposition “n is an even number” could be written
(a) n is the sum of three perfect squares.
Since the constant 0 is not allowed to appear explicitly, the predicate “” can’t be written directly, but note that it could be expressed in a simple way as:
Then the predicate could be expressed
Note that we’ve used “” in this formula, even though it’s technically not allowed. But since “” is equivalent to the allowed formula “,” we can use “” with the understanding that it abbreviates the real thing. And now that we’ve shown how to express “”, it’s ok to use it too.
(b) .
(c) is a prime number.
(d) is a product of two distinct primes.
(e) There is no largest prime number.
(f) (Goldbach Conjecture) Every even natural number can be expressed as the sum of two primes.
(g) (Bertrand’s Postulate) If , then there is always at least one prime such that .
¶ Solution (My own answers probably wrong regarding valid quantifier syntax, loop back to this)
a)
b) A unique property of one is that multiplying one by itself is idempotent. Adding one to itself is not. Also, squaring one equals itself. Any number greater than one, when we square it, will be greater than the value we squared.
We define as and then express as
c) If a number is prime, it is greater than 0 and there are no numbers and that add to it.
IS-PRIME
d) n is a product of two numbers, which themselves are numbers for which there does not exist two numbers that add up to them.
e) There is no largest prime number.
IS-PRIME IS-PRIME
"There does not exist a prime number and for all numbers , if is prime then p is greater than ."
f) (Goldbach Conjecture) Every even natural number can be expressed as the sum of two primes.
Define a proposition Is-Two(n) using the fact that two is the only number that Is-Prime and Is-Even (we can use this proposition since its in the question description)
Using the n > 1 and Is-Two estalished above...
My answer is missing the actual implication part...
We can define with the formula . can be expressed as . The conjecture can be expressed as:
g) (Bertrand’s Postulate) If , then there is always at least one prime such that .
IS-PRIME
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 4
If a set, , is finite, then , and so there is no surjection from set to its powerset. Show that this is still true if is infinite. Hint: Remember Russel's paradox and consider where is such a surjection.
¶ Solution
Scratch: Proving by contradiction.
Suppose there was a surjective function that maps a set to its powerset .
Let be the set of in that are not in the image of .
So by definition we get the following biconditional for all in .. if is in that means that isn't in the image of and if isn't in the image of that means its in .
We know that every element of is in by the definition of the subset of a set.
This means that is also a member of by the definition of a powerset (the powerset contains all subsets of its set, is a subset of so obviously it will be in the powerset as well).
Since is a surjection from to , there exists some in whose image is .
So by our earlier biconditional we can replace with and get
Substituting for yields a contradiction, proving there cannot be such an .
Proof:
Proof by contradiction. Suppose there was a surjection for some set . Let . So by definition
for all . But by definition and hence is a member of ). This means that for some , since is a surjection to . So we have from
for all . Substituting for in yields a contradiction, proving there cannot be such an .
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 5
(a) Prove that
is valid.
(b) Prove that the converse of is not valid by describing a counter model as in Week 2 Notes.
¶ Solution (From book)
(a)
Assume
That is, holds for some element of the domain. Let be this element, that is, we have .
In particular, holds by itself. So we conclude (By Existential Generalization) . We conclude similarly. Hence,
holds. This shows that holds in any interpretation in which holds. Therefore, implies in all interpretations, that is valid.
(b)
We describe a counter model in which is true and is false.
Let the domain be , mean "", and mean "". Then, is true (let be ) and likewise is true (let be ), so holds.
On the other hand, is not true, so is not true. Likewise, is not true. Since these are the only elements of , it is not true that there is an element, , of , such that . That is, is not true.
¶ Scratch
The proposition states that if there exists some for which and are true then there exists some for which is true and there exists some y for which is true.
Let be the domain for the variables and , and be some unary predicates on .
We need to show that if holds, then so does .
So suppose . So some element has the property that is true.
Suppose . There exists some that has the property is true and there exists some that is true.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 Problem Set 1 Problem 6
(a) Give an exmaple where the following result fails:
False Theorem: For sets , , , and , let
Then .
(b) Identify the mistake in the following proof of the False Theorem.
Bogus proof: Since and are both sets of pairs, its sufficient to prove that for all .
The proof will be a chain of iff implications. (ignore crappy alignment)
and ,
either or and either or ,
and or else and
or
(c) Fix the proof to show that .
¶ Solution
Scratch:
and are sets of ordered pairs.
is the cartesian product of the unions of sets and and and .
or
is the union of the cartesian product of and and the cartesian product of and .
or
Example where it fails:
set a: a, b, c, d
set b: d, e, f
set c: 1, 2, 3
set d: 4, 5, 6
u1 = {a,b,c,d} ∪ {1,2,3} = {a,b,c,d,1,2,3}.
u2 = b u d {d,e,f} ∪ {4,5,6} = {d,e,f,4,5,6}.
l = u1 x u2 = {{a,d},{a,e},{a,f},{a,4},{a,5},{a,6},{b,d},{b,e},{b,f},{b,4},{b,5},{b,6},{c,d},{c,e},{c,f},{c,4},{c,5},{c,6},{d,d},{d,e},{d,f},{d,4},{d,5},{d,6},{1,d},{1,e},{1,f},{1,4},{1,5},{1,6},{2,d},{2,e},{2,f},{2,4},{2,5},{2,6},{3,d},{3,e},{3,f},{3,4},{3,5},{3,6}}
cp1 = {{a,d},{a, e},{a, f},{ b,d},{ b, e},{ b, f},{ c,d},{ c, e},{ c, f},{ d,d},{ d, e},{ d, f}}
cp2 = {{1,4},{1, 5},{1, 6},{ 2,4},{ 2, 5},{ 2, 6},{ 3,4},{ 3, 5},{ 3, 6}}
r = cp1 u cp2 {{a,d},{a, e},{a, f},{ b,d},{ b, e},{ b, f},{ c,d},{ c, e},{ c, f},{ d,d},{ d, e},{ d, f}, {1,4},{1, 5},{1, 6},{ 2,4},{ 2, 5},{ 2, 6},{ 3,4},{ 3, 5},{ 3, 6}}
a: If = = and and are both nonempty, then , but .
b: It does not necessarily follow that . may be in or instead.
d:
Proof: (ignore crappy alignment)
and ,
either or and either or ,
and or else and
or
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 In-Class Problems Week 1 Problem 1
Identify exactly where the bugs are in each of the following bogus proofs.
(a)
Bogus Proof
and the claim now follows by the rules for multiplying fractions.
(b)
¶ Solution
(a) The symbol on the second line should be switched to because is negative.
(b) There is mismatching going on between and
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 In-Class Problems Week 1 Problem 2
Proposition: (Arithmetic-Geometric Mean Inequality) For all nonnegative real numbers and
What is wrong with the following proof of this proposition?
Bogus Proof
The last statement is true because is a real number, and the square ofa real number is never negative. This proves the claim
¶ Solution
The proof doesn't prove that the Arithmetic-Geometric Mean Inequality claim. It just proves which is not very interesting since we already know the square of any nonnegative number is nonnegative.
The big problem here with the bogus proof as it is written, is that it reasons backwards, beginning with the proposition in question and reasoning to a true conclusion.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2005 In-Class Problems Week 3 Problem 1
Generalize the proof that is irrational to extend to, for example, cube roots of . Remember that an irrational number is a number that cannot be expressed as a ratio of two integers.
Theorem: is an irrational number.
Proof: The prof is by contradiction. Assume for purpose of contradiction that is rational.
Then we can write where and are integers and the fraction is in lowest terms. Squaring both sides gives , so . This implies that is even, and hence that is even; that is, is a multiple of . That means is actually a multiple of , say .
Now we have , so . So is even, and hence is even. But since and are both even, the fraction is not in lowest terms, a contradiction. .
¶ Solution
We prove by contradiction that for any , is irrational.
Assume for the prupose of contradiction that is rational.
Then we can write where and are integers and the fraction is in lowest terms.
Raising both sides by gives
so . This implies that is even, and hence is even and also a multiple of .But that means is actually a multiple of , say .
Now we have , so . So is even, and hence is even. But since and are both even, the fraction is not in lowest terms, a contradiction.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2015 Problem Set 1 Problem 1
Prove that is irrational
¶ Solution
Proof by Contradiction:
Assume to the contrary that is rational, so there are two integers and where .
This can be rewritten as
We get an even number raised to an exponent equal to an odd number raised to an exponent. This is a contradiction, so must be irrational.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2015 Problem Set 1 Problem 2
Use the Well Ordering Principle to prove that
for every nonnegative integer .
Hint: Verify for by explicit calculation.
¶ Solution
Proof:
Let be the least element .
We know that the theorem is false for but true for all nonnegative integers . We can verify directly that for , so we must have .
must be true...
must be false. its the smallest for which the proposition is false.
¶ MIT OCW 6.042J Mathematics for Computer Science Fall 2015 Problem Set 1 Problem 3
a: Verify by truth table that
¶ Discrete Math Workbook 3rd Edition Section 3.2 Question 6
Prove is irrational.
¶ Answer
Proof:
Proof by contradiction. Assume is rational, so there exists where .
Square both sides
It is obvious that must be a multiple of 3, so must as well. So for some , . Plug into our above equation..
Both and are divisible by , so they are not coprime integers and they must not be in most reduced form, which is a contradiction. Therefore must be irrational.
¶ Discrete Math Workbook 3rd Edition Section 3.2 Question 2
For each of the statements below, say what method of proof you should use to prove them. Then say how the proof starts and how it ends. Bonus points for filling in the middle.
- There are no integers and such that is a prime greater than and .
- For all integers , if is a multiple of , then can be written as the sum of consecutive integers.
- For all integers and , if is odd, then or is odd.
¶ Solution
-
Proof by contradiction. Assume there are integers and where is a prime greater than and . This implies is a divisible by 3, since is an integer that is multiplied by a multiple of 3 and has 3 added to it. Since is divisible by a number besides 1 and itself, this is a contradiction to our initial assumption. Therefore and do not exist.
-
Direct Proof. Assume is a multiple of and there are some consecutive integers , , and that sum to n. So we have
We see that is equal to the sum of three consecutive integers. That sum can be represented as an integer which itself is a multiple of , so must be a multiple of .
3. Proof by contrapositive. If and are even, then is even. There are some numbers and such that and . So we get
Since is an integer, that is a multiple of 4, so it is even. Therefore, is even.
¶ Discrete Math Workbook 3rd Edition Section 3.2 Question 3
Consider the statement: for all integers , if is even then is even.
a. Prove the statement. What sort of proof are you using?
b. Is the converse true? Prove or disprove.
¶ Solution
a. Using a direct proof, assume is even. So there exists some integer that . We get , therefore is even.
b. The converse of this statement is false. It fails when , or .
¶ Discrete Math Workbook 3rd Edition Section 3.2 Question 4
The game TENZI comes with six-sided dice (each numbered to ). Suppose you roll all dice.
a. Prove that there will be at least seven dice that land on the same number.
b. How many dice would you have to roll before you were guaranteed that some four of them would all match or all be different? Prove your answer.
¶ Solution
a. Proof by contradiction. Suppose we roll sided dice, no more than dice will land on the same number. That means that we have rolled, at the most, dice. This is a contradiction, proving our claim that there will be at least dice with the same result.
b. Proof by contradiction. Suppose you roll dice, but that there are no more than rolls that match or are all different. That means at most, there are of any given value. If we had just different values, that would be only dice, so there must be different values, giving dice that are all different.
¶ Discrete Math Workbook 3rd Edition Section 3.2 Question 7
¶ Solution
Consider the statement: for all integers and , if is even and is a multiple of , then is a multiple of .
a) Prove the statement. What sort of proof are you using?
b) State the converse. Is it true? Prove or disprove.
¶ Solution
a) Direct Proof. for some integer . for some integer . From that we get
and are an integer that is a multiple of .
b) The converse is, "If is a multiple of , then is even and is a multiple of ". The converse is false. Consider the case and . which is a multiple of and is a multiple of , but is odd.
¶ How to Prove it A Structured Approach: Second Edition Section 3.1 Question 6
Suppose and are real numbers. Prove that if then .
¶ Solution
Proof: We can multiply both sides of the inequality by the positive number , resulting in . This can be reduced to .
¶ How to Prove it A Structured Approach: Second Edition Section 3.1 Question 7
Suppose that is a real number. Prove that if then . (Hint: One approach is to start by completing the following equation
¶ Solution
Assume . Subtracting from both sides we get
Multiply both sides by
Add to both sides to get
¶ How to Prove it A Structured Approach: Second Edition Section 3.1 Question 8
Suppose and . Prove that if then .
¶ Solution -- TODO finish this one
Theorem: If , , and , then
Scratch:
- Convert given into definitions for (difference, subset, intersection)
- For we have
-
Suppose the contrapositive, that .
-
Since we assume and we suppose , by 2 we have
-
Conc?
Proof: We prove the contrapositive. Suppose . Then from we can conclude .
¶ Book of Proof Chapter 8 Exercise 1
Prove that
¶ Solution
Here we have to prove that the set of integers that are multiples of 12 are a subset of integers that are both multiples of 2 and 3
-
Suppose
-
This means that for some in .
-
Therefore, and ).
-
From it follows that is a multiple of , so .
-
From it follows that is a multiple of , so
-
By the definition of intersection of two sets we have
- Thus
¶ Book of Proof Chapter 8 Exercise 3
If , then
¶ Solution
Scratch:
(Prove that
Proof:
-
Suppose .
-
This means that and .
-
By definition of divisibility, there is an integer for which .
-
Squaring both sides we get
-
We see by is divisible by . This means that
-
We have shown that
¶ Book of Proof Chapter 8 Exercise 5
If and are positive integers, then
¶ Solution
Scratch: Need to prove the intersection of multiples of and multiples of is nonempty.
Proof:
- Suppose and are integers. Consider the integer .
- Observe that and , so .
- Therefore
¶ Book of Proof Chapter 8 Exercise 7
Suppose , , and are sets. If , then
¶ Solution
Scratch: We need to prove if .
Proof:
- Suppose .
- This means that and .
- Suppose
- This means that
- Since and , we have
- We've shown , so
¶ Book of Proof Chapter 8 Exercise 9
If , and are sets, then
¶ Solution
Note: Distributive law
Proof:
Line 1: intersection
Line 2: union
Line 3: Distributive law
Line 4: intersection
Line 5 union
¶ Book of Proof Chapter 8 Exercise 11
If . and are sets in a universal set , then ,
¶ Solution
scratch:
- Definition of complement
- Definition of union
- ??
Last) ?? Conclusion
¶ Solution (from book)
Proof: Observe the following sequence of equalities
Line 1: def of complement
Line 2: Definition of set difference
Line 3: Rewrite to logical equivalence
Line 4: Definition of union
Line 5: DeMorgans Law
Line 6: Rewrite to logical equivalence
Line 7:
Line 8: regroup
Line 9: Definition of intersection
Line 10: Definition of set difference
Line 11: Definition of compliment
¶ Book of Proof Chapter 8 Exercise 19
Prove that but
¶ Solution
Proof:
¶ Book of Proof Chapter 8 Exercise 21
Suppose and are sets. Prove