¶ Partial Orderings
A relation on a set is called a partial ordering or partial order if it is reflexive, antisymmetric, and transitive. A set together with a partial ordering is called a partially ordered set, or poset, and is denoted by . Members of are called elements of the poset.
¶ Antisymmetry
Let be a relation on a set is antisymmetric if, and only if, for every and in if and then .
In terms of an arrow diagram of a relation, saying that a relation is antisymmetric is the same as saying that whenever there is an arrow goign from one element to another distinct element, there is not an arrow going back from the second to the first.
¶ Example: Testing for Antisymmetry of "Divides" Relations
Let be the "divides" relation on the set of all positive integers, and be the "divides" relation on the set of all integers. Prove or give a counterexample of and being antisymmetric.
is antisymmetric.
Proof: Suppose and are positive integers such that and . [We must show that By definition of and . Thus, by definition of divides, there are integers and with and . It follows that
Dividing both sides by gives
Now since and are both integers, and are both positive integers also. And the only product of two positive integers that equals 1 is . Thus
and so
[as was to be shown].
is not antisymmetric. Let and . Then since and [since . Hence and but .
¶ Example: Show that the greater than or equal to relation is a partial ordering on the set of integers
Because for every integer is reflexive. If and , then . Hence, is antisymmetric. Finally, is transitive because and imply that . It follows that is a partial ordering on the set of integers and is a poset.
¶ Example: Show that the inclusion relation is a partial ordering on the power set of a set .
Because whenever is a subset of is reflexive. It is antisymmetric because and imply that . Finally, is transitive, because and imply that . Hence, is a partial ordering on , and is a poset.
¶ Comparability and Totally Ordered sets
Suppose is a partial order relation on a set . Elements and of are said to be comparable if, and only if, either or . Otherwise, and are called noncomparable.
Given any two real numbers and , either or . The elements and in this case are comparable.
Given two subsets and of , it may be the case that neither nor . For instance, let and Then and In such a case, and are said to be noncomparable.
When every two elements in the set are comparable, the relation is called a total ordering.
If is a poset and every two elements of are comparable, is called a totally ordered or linearly ordered set, and is called a total order or a linear order. A totally ordered set is also called a chain. The length of a chain is one less than the number of elements in the chain.
A set that is partially ordered but not totally ordered may have totally ordered subsets. Such subsets are chains.
¶ Chain Length Subsets Example
The set is partially ordered with respect to the subset relation. Find a chain of length 3 in
Solution Since , the set
is a chain of length 3 in
¶ Maximal and Minimal Elements
Maximal and minimal elements are easy to spot using a Hasse diagram. They are the "top" and "bottom" elements in the diagram.
¶ Maximal
An element of a poset is called maximal if it is not less than any element of the poset. That is, a is maximal in the poset if there is no such that .
An element in is called a maximal element of if, and only if, for each in , either or and are not comparable.
¶ Greatest
An element in is called a greatest element of if, and only if, for each in
¶ Minimal
Similarly, an element of a poset is called minimal if it is not greater than any element of the poset. That is, is minimal if there is no element such that .
An element in is called a minimal element of if, and only if, for each in , either or and are not comparable.
¶ Least
An element in is called a least element of if, and only if, for each in , .
¶ Example - Identifying minimal and maximal elements of a set
(a) What are the maximal and minimal elements, if any, of the set, , of all natural numbers under divisibility? Is there a minimum or maximum element?
(b) What are the minimal and maximal elements, if any, of the set of integers under divisibility?
¶ Solution
(a) The minimum (and therefore unique minimal) element is 1 since 1 divides all natural numbers. The maximum (and therefore unique maximal) element is 0 since all numbers divide
(b) All prime numbers are minimal elements, since no numbers divide them. Since there is more than one minimal element, there can't be a minimum element. There is no maximal element, because for any , there is a "larger" number under the divisibility partial order, namely, , for any .
¶ Well Ordered Set
is a well-ordered set if it is a poset such that is a total ordering and every nonempty subset of has a least element.
¶ Lexicographic Order
Let be a set with a partial order relation , and let be a set of strings over Define a relation on as follows:
Let and be any strings in of lengths and , respectively, where and are positive integers, and let and be the characters in the th position for and , respectively.
- If and the first characters of and are the same, then .
- If the first characters in and are the same, , and , then .
- If is the null string then .
If no strings are related by other than by these three conditions, then is a partial order relation on .
¶ Example - Testing Strings for Lexicographic Order
Let and let be the following partial order relation on :
Let be the set of all strings over , and denote by the lexicographic order for that corresponds to .
a. Is Is Is ?
b. Is ?
c. Is ?
d. Is ?
e. Is ?
¶ Solution - Testing Strings for Lexicographic Order
a. Yes in all three cases, by property (1) of the definition of
b. Yes in all cases, by property (2) of the definition of .
c. Yes in all cases, by property (2) of the definition of . In this case , and the statement that the first zero characters of and are the same is true by default.
d. Yes by property (3) of the definition of
e. No because is not related to by .
¶ Hasse Diagrams
A Hasse diagram is a digraph for a finite poset that has mandatory edges removed.
-
Digraph for the partial ordering on the set .
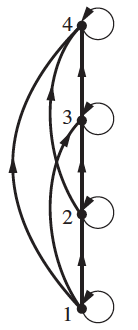
-
Remove the mandatory reflexive relation self loops on vertices.
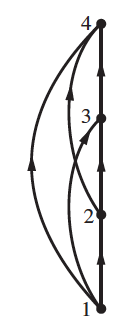
-
Remove transitive edges, because they must be present, and remove direction because we assume all edges are pointed "upwards".
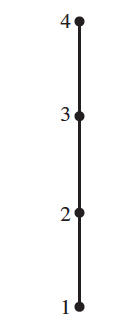
¶ Representing a finite poset using a Hasse Diagram
- Start with the directed graph for the relation.
- Remove reflexive loops.
- Remove all edges that must be in the partial ordering because of the presence of other edges and transitivity. That is, remove all edges for which there is an element such that such that and .
- Arrange each edge so that its initial vertex is below its terminal vertex.
- Remove all arrows on the directed edges, because all edges point "upward" toward their terminal vertex.
¶ Covering Relation
Let be a poset. We say that an element covers an element if and there is no element such that The set of pairs such that covers is called the covering relation of . From the description of the Hasse diagram of a poset, we see that the edges in the Hasse diagram of are upwardly pointing edges corresponding to the pairs in the covering relation of . Furthermore, we can recover a poset from its covering relation, because it is the reflexive transitive closure of its covering relation. This tells us that we can construct a partial ordering from its Hasse diagram.
¶ Recovering a directed graph from the Hasse Diagram
- Reinsert the direction markers on the arrows making all arrows point upward.
- Add loops at each vertex.
- For each sequence of arrows from one point to a second and from that second point to a third, add an arrow from the first point to the third.
¶ Topological Sorting
Suppose a project is made up of 20 different tasks that can be completed only after others have been finished. How can an order be found for these tasks?
To model this problem we set up a partial order on the set of tasks so that iff and are tasks where cannot be started until has been completed. To produce a schedule for the project, we need to produce an order for all tasks that is compatible with this partial order.
¶ Definition
A total ordering is said to be compatible with the partial ordering if whenever Constructing a compatible total ordering from a partial ordering is called topological sorting.
Lemma: Every finite nonempty poset has at least one minimal element.
Proof: Choose an element of . If is not minimal, then there is an element with . If is not minimal, there is an element with . Continue this process, so that if is not minimal, there is an element with Because there are only a finite number of elements in the poset, this process must end with a minimal element .
¶ Algorithm
Let be a partial order relation on a nonempty finite set To construct a topological sorting:
- Pick any minimal element in [Such an element exists since is nonempty.]
- Set .
- Repeat steps while
a. Pick any minimal element in .
b. Define .
c. and .
[Completion of steps of this algorithm gives enough information to construct the Hasse diagram for the total ordering . We have already shown how to use the Hasse diagram to obtain a complete directed graph for a relation.