¶ Induction
Induction proofs have two parts.
- Show that the statement holds for the positive integer . (the basis step)
- Show that the statement holds for the next larger integer. ( is true for all positive integers , the inductive step).
Induction is based on the rule of inference that tells us that if and are true for the domain of positive integers, then is true.
Induction can be used only to prove results obtained some other way. It is not a tool for discovering formulae or theorems.
Expressed as a rule of inference, induction can be stated as
Mathmatical induction relies on the Well Ordering Principle.
¶ Template for Proofs by Mathematical Induction
-
Express the statement that is to be proved in the form "for all ", for a fixed integer . For statements of the form " for all positive integers , let . For statements of the form " for all nonnegative integters ", let . For some statements of the form , such as inequalities, you may need to determine the appropriate value of by checking the truth tables of for small values of .
-
Write out the words "Basis Step". Then show is true, taking care that the correct value of is used.
-
Write out the words "Inductive Step", and state the inductive hypothesis in the form, "Assume is true for an arbitrary fixed integer ."
-
State what needs to be proved under the assumption that the inductive hypothesis is true. That is, write out what says.
-
Prove the statement making use of the assumption . Be sure that your proof is valid for all integers with , taking care that the proof works for small values of , including .
-
Clearly identify the conclusion of the inductive step, such as by saying, "This completes the inductive step."
-
After completing the basis and inductive step, state the conclusion, "By mathematical induction, is true for all integers with .
¶ Examples
¶ Proving Summation Formulae
Keep in mind that induction can't be used to derive a summation formula. We must already have the formukla before we can attempt to prove it by induction.
¶ Example 1
Show that if is a positive integer, then
Basis Step: is true because .
Inductive Step: For the inductive hypothesis we assume that holds for an arbitrary positive integer . That is, we assume
Under this assumption, it must be shown that is true, namely, that
is also true.
We now look ahead to see how we might be able to prove that holds under the assumption that is true.We observe that the summation in the left-hand side of is
more than the summation in the left-hand side of . Our strategy will be to add to
both sides of the equation in and simplify the result algebraically to complete the inductive step.
Returning to the inductive step of the proof, when we add to both sides of the equation , we obtain
The last equation shows that is true udner the assumption that is true. This completes the inductive step.
We have completed the basis and the inductive step, so by mathematical induction we know that is true for all positive integers . That is, we have proven that for all positive integers .
¶ Example 2
Conjecture a formula for the sum of the first n positive odd integers. Then prove your conjecture using mathematical induction.
The sums of the first positive integers for are , , , ,
From these values its reasonable to conjecture that our formula for the sum of the first positive integers is .
Let denote the proposition that the sum of the first odd positive integers is . Conjecture is that is true for all positive integers .
Basis Step: = 1
Inductive Step: We must show that is true for every positive integer . To do this, we assume the inductive hypothesis ( that is true for every positive integer , that is,
)
To show that is true, we must show that is true, then is true. Note that is
We need to look for a way to use the inductive hypothesis to show that is true. is the sum of its first terms and its last term . So we can use our inductive hypothesis to replace by .
Returning to the proof, we find that
This shows that follows from . Note that we used the inductive hypothesis in the second equality to replace the sum of the first odd positive integers by .
We have now completed both the basis step and the inductive step. We have shown that is true and the conditional statement is true for all positive integers . Consequently, by the principle of mathematical induction we can conclude that is true for all positive integers . That is, we know that for all positive integers .
¶ Proving Inequalities
A trick that is occasionally useful for proving inequalities is adding unequal quantities to both sides of an inequality, as long as the quantity added to the bigger side is bigger than the quantity added to the smaller side.
¶ Example using the add unequal quantities trick
The inequality
holds for each .
Base Case: , simplifies to , which is obviously true.
Inductive Step:
Say . We use direct proof to show that . Suppose . Then..
It follows by induction that for each .
¶ Example
Use mathematical induction to prove the inequality
for all positive integers .
Let be the proposition that .
Basis Step: is true, because . This completes the basis step.
Inductive Step: We assume the inductive hypothesis is true for some arbitrary integer . To complete the inductive step, we need to show that if is true, then , which is the statement that is true. That is, we need to show if , then . To show that this conditional statement is true for the positive integer , we first add to both sides of , and then note that . This tells us that
This shows that is true, namely that , based on the assumption that is true.
Therefore, because we have completed both the basis step and the inductive step, by the principle of mathematical induction we have shown that is true for all positive integers .
¶ Proving Divisibility Results / Properties
¶ Example
Prove that for each integer , is divisible by .
Let denote the proposition "" is divisible by .
Base Case: . is divisible by so this holds.
Inductive Hypothesis: is true.
Inductive Step: Assuming is true we need to prove where .
There is some where .
¶ Example
Use mathematical induction to prove that is divisible by for every nonnegative integer .
Let denote the proposition " is divisible by "
Base Case: is divisible by .
Inductive Step: We assume is true for an arbitrary nonnegative integer , that is, we assume is divisible by .
We aim to prove , where is the statement that is divisible by .
We can now use the inductive hypothesis, which states that is divisible by . We will use the following theorems for the rest of the proof:
- (i) if and , then
- (ii) if , then for all integers
By ii and the inductive hypothesis, we conclude that the first term in the last sum, , is divisible by . By ii, the second term, , is divisible by . By part i, we conclude that is divisible by . This completes the inductive step.
Because we have completed the base and inductive steps, by mathemtical induction we know that is divisible by for every nonnegative integer .
¶ Example
Prove that for any odd number , the number divides .
Base case is .
Since is odd it can be written as for some (definition of odd number). So for our theorem we have or
We need to show is also divisible by .
Hence is also divisible by .
¶ Proving Results About Sets
¶ Example - The Number of Subsets of a Finite Set
Use induction to show that if a set is a finite set with elements, where is a nonnegative integer, then has subsets.
Solution: Let be the proposition that a set with elements has subsets.
Basis Step: is true, because a set with elements, the empty set, has subsets, itself.
Inductive Step: We assume that is true for an arbitrary nonnegative integer , that is, we assume evry set with elements has subsets. We must show $P(k) \rarr , that is, every set with elements has subsets.
To show this, let be a set with elements. Then we can write , where is one of the elements of and (hence ). The subsets of can be obtained in the followingt way. For each subset of there are exactly two subsets of , namely and (illustrated below). 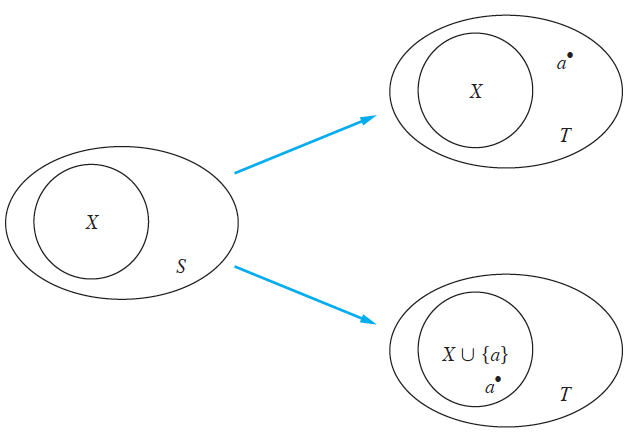
These constitute all the subsets of and are all distinct. We now use the inductive hypothesis to conclud e that has subsets, because it as elements. We also know there are two subsets of for each subset of . Therefore, there are subsets of . This finishes the inductive argument.
Because we have completed the basis and inductive step, by induction it follows that is truef or all nonnegative integers .
¶ Proving Results About Algorithms
¶ Examples
¶ Proving a greedy algorithm always produces an optimal solution
Consider an algorithm to schedule talks that have preset start and end times. The algorithm schedules as many talks as possible in a lecture hall, under the assumption that once a talk starts, it continues until it ends, and only one talk can proceed at a time. A talk can begin at the same time another one ends.
The input of the algorithm is a group of proposed talks with preset starting and end times. Suppose that talk begins at time and ends at time .
Without loss of generality, we assume that the talks are listed in order of nondecreasing ending time, so that . The greedy algorithm proceeds by selecting at each stage a talk with the earliest ending time among all those talks that begin no sooner than when the last talk scheduled in the main lecture hall has ended. Note that a talk with the earliest end time is always selected first by the algorithm.We will show that this greedy algorithm is optimal in the sense that it always schedules the most talks possible in the main lecture hall. To prove the optimality of this algorithm we use mathematical induction on the variable , the number of talks scheduled by the algorithm. We let be the proposition that if the greedy algorithm schedules talks in the main lecture hall, then it is not possible to schedule more than talks in this hall.
Base Step: Suppose the greedy algorithm managed to schedule just one talk, , in the lecture hall. This means that no other talk can start at or after , the end time of . Otherwise, the first such talk we come to as we go through the talks in order of nondecreasing end times could be added. Hence, at time each of the remaining talks start before and end after . It follows that no two talks can be scheduled because both need to use the same lecture hall at time . This shows that is true and completes the basis step.
Inductive Step:
The inductive hypothesis is that is true, where is an arbitrary positive
integer, that is, that the greedy algorithm always schedules the most possible talks when it selects
talks, where is a positive integer, given any set of talks, no matter how many.We must show
that follows from the assumption that is true, that is, we must show that under
the assumption of , the greedy algorithm always schedules the most possible talks when it
selects talks.
Now suppose that the greedy algorithm has selected talks. Our first step in completing
the inductive step is to show there is a schedule including the most talks possible that contains
talk , a talk with the earliest end time. This is easy to see because a schedule that begins
with the talk in the list, where , can be changed so that talk replaces talk . To see
this, note that because , all talks that were scheduled to follow talk can still be scheduled.
Once we included talk , scheduling the talks so that as many as possible are scheduled
is reduced to scheduling as many talks as possible that begin at or after time . So, if we
have scheduled as many talks as possible, the schedule of talks other than talk is an optimal schedule of the original talks that begin once talk has ended. Because the greedy algorithm
schedules talks when it creates this schedule, we can apply the inductive hypothesis to conclude
that it has scheduled the most possible talks. It follows that the greedy algorithm has scheduled
the most possible talks, , when it produced a schedule with talks, so is
true. This completes the inductive step.
We have completed the basis step and the inductive step. So, by mathematical induction we
know that is true for all positive integers . This completes the proof of optimality. That is,
we have proved that when the greedy algorithm schedules talks, when is a positive integer,
then it is not possible to schedule more than talks.
¶ Courtyard Tiling
Picture a grid.
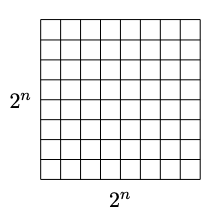
One of the central squares in the grid will be occupied by a statue(Let's call it Bob's statue, or B). In the special case , the whole courtyard consists of a single central square; otherwise there are four central squares.
A complication is that the architect of this grid courtyard insists on only special L-shaped tiles are to be used.
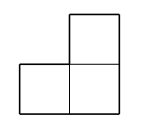
A courtyard meeting these constrains exists, at least for .
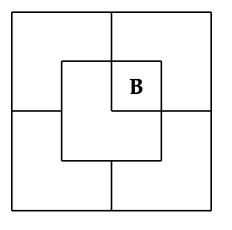
For larger values of , is there a way to tile a courtyard with L-shaped tiles and a statue in the center? Let's try to prove that this is so.
Theorem 1: For all there exists a tiling of a courtyard with a Bob statue in a central square.
Proof: This proof is by induction. Let be the proposition that for every location of Bob in a courtyard, there exists a tiling of the remainder.
Base Case: is true because Bob fits the whole courtyard.
Inductive Step: Assume that is true for some ; that is, for every location of Bob in a courtyard, there exists a tiling of the remainder. Divide the courtyard into four quadrants, each . One quadrant contains Bob (B in the diagram). Place a temporary Bob (X in the diagram) in each of the three central squares lying outside this quadrant:
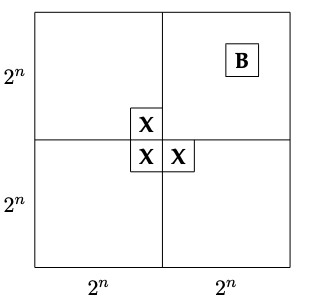
Now we can tile each of the four quadrants by the induction assumption. Replacing the three temporary Bobs with a single L-shaped tile completes the job. This proves that for all . The theorem follows as a special case.
¶ Strong Induction
In a proof by strong induction, the inductive step shows that if is true for all positive integers not exceeding , then is true. That is, for the inductive hypothesis we assume that is true for .
In other words, to prove is true for all positive integers , where is a propositional function, we complete two steps:
-
Basis Step: We verify that the proposition is true.
-
Inductive Step: We show that the conditional statement is true for all positive integers .
¶ Examples
¶ Products of Primes
Lemma 1: Every integer greater than is a product of primes.
Proof: Our induction hypothesis
So our lemma will follow if we prove that holds for all .
Base Case: is true because is prime, and so is a product of primes by convention.
Inductive Step: Suppose that and that is a product of primes for every natrual number . We must show that holds, namely, that is also a product of primes. We argue by cases:
If is itself prime, then it is a product of primes by convention, so holds in this case.
Otherwise, is not prime, which means that for some natural numbers such that . So is a natural number less than , which means that is a product of primes by induction hypothesis. That is, is a product of primes. Likewise, is a product of primes. So is also a prioduct of primes. Therefore holds in this case as well.
So holds in any case, which completes the proof by strong induction that holds for all natural numbers .