¶ Graphs and Graph Models
A graph consists of , a nonempty set of vertices (or nodes) and , a set of edges. Each edge has either one or two vertices associated with it, called its endpoints. An edge is said to connect its endpoints.
A graph can either be finite or infinite. They have finite vertex set or infinite vertex set respectively.
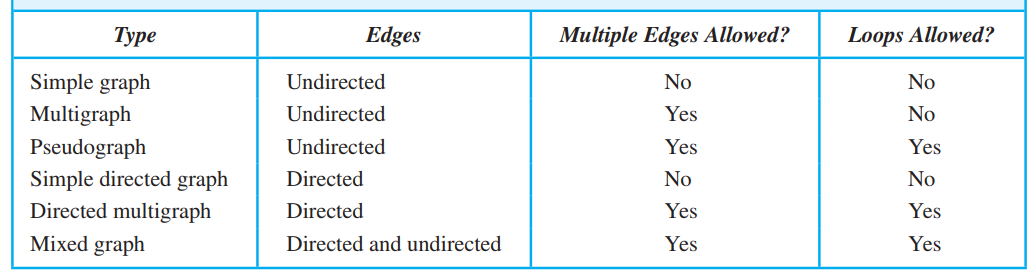
¶ Types of graphs
¶ Graph Models
Graphs can be used to model
- social networks
- communication (telephone, computer etc..) networks
- information networks
- transportation networks (airline routes, shipping, rail networks etc..)
- program dependencies - each module is represented by a vertex. There is a directed edge from a module to a second module if the second module depends on the first.
- statement precedence (execution orders for a program) - Some statements may require the output of previously executed statements, and such a graph of statements would be represented by a digraph. Each statement would be a node in the graph, and there would be an edge from one statement to a second statement if the second statement cannot be executed before the first statement is.
- biological networks
- niche overlap graph (models competition between species in an environment)
- protein interaction graphs
- Semantic networks ( natural language understanding )
- Tournaments
- Round robin
- Single Elimination
- Sexual partners