¶ Directed Graph / Digraph
A directed graph / digraph consists of a set of of vertices (or nodes) together with a set of ordered pairs of elements of called edges (or arcs). The vertex is called the initial vertex of the edge and vertex is called the terminal vertex of this edge.
An edge of the form is representing using an arc from the vertex back to itself. Such an edge is called a loop.
A directed graph is the same as a binary relation on a set , but we picture the digraph geometrically by representing elements of as points on the plane, with an arrow from the point for to the point for exactly when . The elements of are referred to as the vertices of the digraph.
Below, the divisibility relation on is represented by the following digraph:
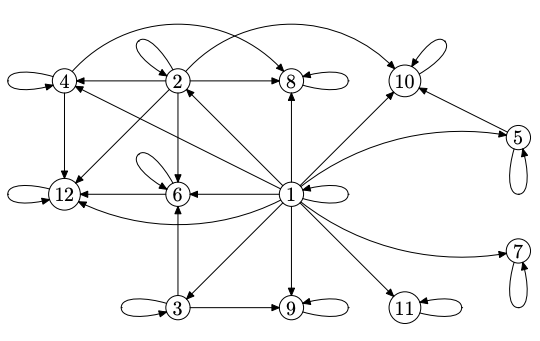
¶ Paths in Digraphs
A path in a digraph, , is a sequence of vertices , with such that , for every . The path is said to start at , to end at , and the length of the path is defined to be .
Many of the relation properties have geometric descriptions in terms of digraphs. For example:
Reflexivity: All vertices have self loops (a self loop at a vertex is an arrow going from the vertex back to itself)
Irreflexivity: Iff No vertices have selfloops.
Symmetry: Iff All edges are bidirectional.
Antisymmetry: Iff there are never two edges in opposite directions between distinct vertices.
Transitivity: Shortcircuits—for any path through the graph, there is an arrow from the first vertex to the last vertex in the path.
We can define some new relations based on paths. Let be a digraph with vertices, . Define relations and on by the conditions that
is called the path relation of . It follows from the definition of path that is transitive. IT is also reflexive because it has length paths and it contains the graph of because of the length-one paths. is called the positive-length path relation; it also contains graph and is transitive.
¶ Directed Acylic Graphs
Scheduling problems are a common source of partial orders: there is a set of tasks and a set of constraints specifying that starting a certain task depends on other tasks being completed beforehand. We represent the task by vertices and a constraint that task must finish before task can start by an arrow from to .
Below is a directed acylcic graph that describes the order in which to put on clothes.
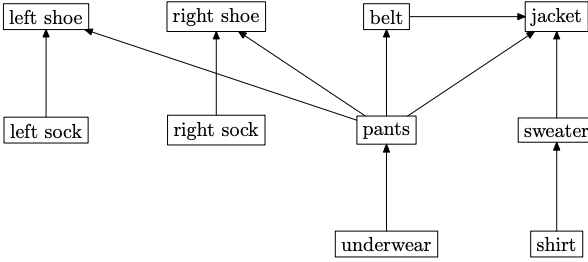
If we were to add a relation from belt to underwear, that would create a cyclic dependency and we would have no way to get dressed.
A cycle is a positive length path in a digraph that begins and ends at the same vertex. A directed acyclic graph is a graph with no cycles.
We use DAG's as an economic way to represent the dependency relation. Usually a task-graph DAG itself is not a transitive relation because it only includes the edges showing "direct" dependencies. Rather, the dependency relation we care about is defined by the positive length path relation, , in the task graph. The dependency relation will always be a partial order.
¶ Topological Sorting
In a DAG for a partial order, incomparable elements appear as vertices with no path between them in either direction. So in a partial order on clothes in the above example, "left shoe" and "right shoe" are incomparable. If the order is total, then the order can be represented by a DAG that looks like a line.
When we have a partial order of tasks to be performed, it can be useful to have an order in which to perform all the tasks, one at a time, while respecting the dependency constraints. This amounts to finding a total order that is consistent with the partial roder. This task of finding a total ordering that is consistent with a partial order is known as topological sorting.
A topological sort of a partial order on a set is a total ordering on such that
A topological sort (one of a few possible) for our dressing example above could be
Topological Sorts for finite DAGs are easy to construct by starting from minimal elements.
¶ Parallel Task Scheduling
Topological sorting provides a way to execute tasks sequentially without violating the dependencies.
A chain in a partial order is a set of elements such that any two elements in the set are comparable.