¶ Undirected Graph Terminology
Two vertices and in an undirected graph are called adjacent (or neighbors) in if and are endpoints of an edge of . Such an edge is called incident with the vertices and and is said to connect and .
The set of all neighbors of a vertex of , denoted by , is called the neighborhood of . If is a subset of , we denote by the set of all vertices in that are adjacent to at least one vertex in So, .
The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex is denoted by .
A vertex of degree zero is isolated.
A vertex of degree one is pendant.
¶ Handshaking Theorem
Let be an undirected graph with edges. Then
(In other words, the sum of the degrees of the vertices in a graph equals twice the number of edges)
(Note that this applies even if multiple edges and loops are present.)
¶ Vertices and Degrees of Undirected Graphsd
An undirected graph has an even number of vertices of odd degree.
Proof: Let and be the set of vertices of even degree and the set of vertices of odd degree, respectively, in an undirected graph with edges. Then
Because is even for , the first term in the right-hand side of the last equality is even. Furthermore, the sum of the two terms on the right-hand side of the last equality is even, because this sum is . Hence, the second term in the sum is also even. Because all the terms in this sum are odd, there must be an even number of such terms. Thus, there are an even number of vertices of odd degree.
¶ Directed Graph Terminology
When is an edge of the graph with directed edges, is said to be adjacent to and is said to be adjacent from . The vertex is called the initial vertex of , and is called the terminal or end vertex of The initial vertex and terminal vertex of a loop are the same.
In a graph with directed edges the in-degree of a vertex , denoted by , is the number of edges with as their terminal vertex. The out-degree of , denoted by , is the number of edges with as their initial vertex. (Note that a loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.)
The undirected graph that results from ignoring directions of edges is called the underlying directed graph.
¶ Sum of in-degrees and out-degrees
The sum of the in-degrees and the sum of the out-degrees of all vertices in a graph with directed edges are the same because each edge has an initial vertex and a terminal vertex. Both of these sums are the number of edges in the graph.
Written in sigma notation..
Let be a graph with directed edges. Then
¶ Special Simple Graphs
¶ Complete Graph
A complete graph on vertices, denoted by , is a simple graph that contains exactly one edge between each pair of distinct vertices. A simple graph for which there is at least one pair of distinct vertex not connected by an edge is called noncomplete.
¶ Cycle
¶ Wheel
¶ n-Cubes
¶ Bipartite Graphs
A simple graph is called bipartite if its vertex set can be partitioned into two disjoint sets and such that every edge in the graph connects a vertex in and a vertex in (so that no edge in connects either two vertices in or two vertices in ). When this condition holds, we call the pair a bipartition of the vertex set of .
A bipartite graph can be colored with only two colors, such that no two adjacent vertices are assigned the same color.
A bipartite graph iff it is not possible to start a vertex and return to this vertex by traversing an odd number of distinct edges.
¶ 2-Coloring and Bipartancy
¶ Theorem
A simple graph is bipartite if and only if it is possible to assign one of two different colors to each vertex of the graph so that no two adjacent vertices are assigned the same color.
¶ Proof
First, suppose that is a bipartite simple graph. Then , where and are disjoint sets and every edge in connects a vertex in and a vertex in . If we assign one color to each vertex in and a second color to each vertex in , then no two adjacent vertices are assigned the same color.
Now suppose that it is possible to assign colors to the vertices of the graph using just two colors so that no two adjacent vertices are assigned the same color. Let be the set of vertices assigned one color and be the set of vertices assigned the other color. Then, and are disjoint and . Furthermore, every edge connects a vertex in and a vertex in because no two adjacent vertices are either both in or both in . Consequently, is bipartite.
¶ Usage
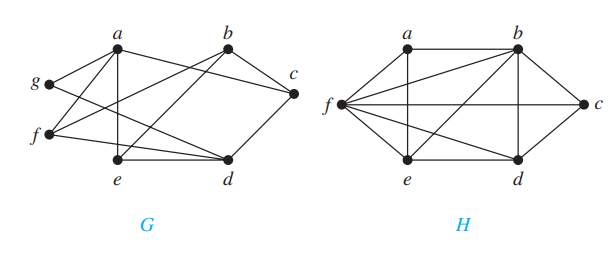
We first consider the graph . We will try to assign one of two colors, say red and blue, to each vertex in so that no edge in connects a red vertex and a blue vertex. Without loss of generality we begin by arbitrarily assigning red to . Then, we must assign blue to , , and , because each of these vertices is adjacent to . To avoid having an edge with two blue endpoints, we must assign red to all the vertices adjacent to either , or . This means that we must assign red to both and (and means that must be assigned red, which it already has been). We have now assigned colors to all vertices, with , and red and , and blue. Checking all edges, we see that every edge connects a red vertex and a blue vertex. Hence, by Theorem 4 the graph is bipartite.
Next, we will try to assign either red or blue to each vertex in so that no edge in connects a red vertex and a blue vertex. Without loss of generality we arbitrarily assign red to . Then, we must assign blue to , and , because each is adjacent to . But this is not possible because and are adjacent, so both cannot be assigned blue. This argument shows that we cannot assign one of two colors to each of the vertices of so that no adjacent vertices are assigned the same color. It follows by Theorem 4 that is not bipartite.
¶ Bipartite Graphs and Matchings
Bipartite graphs can be used to model types of applications that involve matching the elements of one set to elements of another.
¶ Job Assignments
A task like finding an assignment of jobs to employees with the requisite ability can be thought of as finding a matching in the graph model. A matching in a simple graph is a subset of the set of edges of the graph such that no two edges are incident with the same vertex.
In other words, a matching is a subset of edges such that if and are distinct edges of the matching, then , and are distinct.
A vertex that is the endpoint of an edge of a matching is said to be matched in ; otherwise it is said to be unmatched.
A maximum matching is a matching with the largest number of edges. We say that a matching in a bipartite graph with bipartition is a complete matching from to if every vertex in is the endpoint of an edge in the matching, or equivalently, if .
For example, to assign jobs to employees so that the largest number of jobs are assigned employees, we seek a maximum matching in the graph that models employee capabilities. To assign employees to all jobs we seek a complete matching from the set of jobs to the set of employees.
¶ Necessary and Sufficient Conditions For Complete Matchings
¶ Hall's Marriage Theorem
The bipartite graph with bipartition has a complete matching from to if and only if for all subsets of V_
(Recall is the set of all vertices in that are adjacent to at least one vertex in . )
¶ Proof
We first prove the only if part of the theorem. To do so, suppose that there is a complete matching from to . Then, if , for every vertex , there is an edge in connecting to a vertex in . Consequently, there are at least as many vertices in that are neighbors of vertices in as there are vertices in . It follows that .
To prove the if part of the theorem, the more difficult part, we need to show that if for all , then there is a complete matching from to We will use strong induction on to prove this.
Basis step: If , then contains a single vertex Because , there is at least one edge connecting and a vertex Any such edge forms a complete matching from to .
Inductive step: We first state the inductive hypothesis.
Inductive hypothesis: Let be a positive integer. If is a bipartite graph with bipartition , and , then there is a complete matching from to whenever the condition that for all is met.
Now suppose that is a bipartite graph with bipartition and
We will prove that the inductive holds using a proof by cases, using two case. Case applies when for all integers with , the vertices in every set of elements from are adjacent to at least elements of . Case (ii) applies when for some with there is a subset of vertices such that there are exactly neighbors of these vertices in Because either Case (i) or Case (ii) holds, we need only consider these cases to complete the inductive step
Case Suppose that for all integers with , the vertices in every subset of elements from are adjacent to at least elements of . Then, we select a vertex and an element , which must exist by our assumption that We delete and and all edges incident to them from . This produces a bipartite graph with bipartition Because , the inductive hypothesis tells us there is a complete matching from to . Adding the edge from to to this complete matching produces a complete matching from to .
Case (): Suppose that for some with , there is a subset of vertices such that there are exactly neighbors of these vertices in . Let be the set of these neighbors. Then, by the inductive hypothesis there is a complete matching from to Remove these vertices from and and all incident edges to produce a bipartite graph with bipartition
We will show that the graph satisfies the condition for all subsets of . If not, there would be a subset of vertices of where such that the vertices in this subset have fewer than vertices of as neighbors. Then, the set of vertices of consisting of these vertices together with the vertices we removed from has fewer than neighbors in , contradicting the hypothesis that for all . Hence, by the inductive hypothesis, the graph has a complete matching. Combining this complete matching with the complete matching from to , we obtain a complete matching from to .
We have shown that in both cases there is a complete matching from to . This completes the inductive step and completes the proof.
¶ Parallel Processing and Parallel Algorithms
Parallel processing, which uses computers made up of many separate processors, each with its own memory, helps overcome the limitations of computers with a single processor.
Parallel algorithms, which break a problem into a number of subproblems that can be solved concurrently, can then be devised to rapidly solve problems using a computer with multiple processors. In a parallel algorithm, a single instruction stream controls the execution of the algorithm, sending subproblems to different processors, and directs the input and output of these subproblems to the appropriate processors.
¶ Subgraphs
Sometimes we need only part of a graph to solve a problem.
A subgraph of a graph is a graph , where and . A subgraph of is a proper subgraph of if
Let be a simple graph. The subgraph induced by a subset of the vertex set is the graph , where the edge set contains an edge in if and only if both endpoints of this edge are in .
¶ Removing Vertices From a Graph
When we remove a vertex and all edges incident to it from , we produce a subgraph, denoted by . Observe that , where is the set of edges of not incident to . Similarly, if is a subset of , then the graph is the subgraph , where is the set of edges of not incident to a vertex in .
¶ Graph Unions
The union of two simple graphs and is the simple graph with vertex set and edge set . The union of and is denoted by .