¶ Tiling a checkerboard with triominoes
A trionimo (alternately tromino) is made up of three attached squares, which can be of two types: 
Theorem: For any integer , if one square is removed from a checkerboard, the remaining squares can be completely covered by L-shaped trionimoes.
The main insight leading to a proof of this theorem is the observation that because , when a board is is split in half both vertically and horizontally, each half side will have length and so each resulting quadrant will be a checkerboard.
Proof:
We use induction. Let be the sentence
Base Case: is a checkerboard, which is just squares. If one square is removed, the rest form an L shaped trionimo which completely covers the rest of the checkerboard.
Inductive Step: We aim to prove that if is is true.
Let be the sentence
Let be the sentence
Consider a checkerboard with one square removed. Divide it into four equal quadrants. Each will consist of a checkerboard.
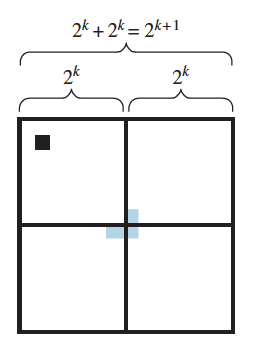
In one of the quadrants, one square will have been removed, and so by the inductive hypothesis, all the remaining squares in this quadrant can be completely covered by L-shaped trionimoes.
The other three quadrants meet at the center of the checkerboard. The center of the checkerboard serves as a corner of a square from each of those quadrants. An L-shaped trionimo can be placed on those three central squares (illustrated above.. note that each of those three quadrants only has 1 square occupied with the placement of the initial trionimo.. the bottom left kind of looks like 2 are shaded).
By inductive hypothesis, the remaining squares in each of the three quadrants can be completely covered by L-shaped trionimoes. Thus every square in the checkerboard except the one that aws removed can be compeltely covered by L-shaped trionimoes.