¶ Types of Closures
If is a relation on a set , it may or may not have some property , such as reflexivity, symmetry, or transitivity. When does not enjoy propety , we would like to find the smallest relation on with property that contains .
If is a relation on a set , then the closure of with respect to , if it exists, is the relation on with property that ocntains and is a subset of every subset containing with property .
¶ Reflexive Closure
The relation on set is not reflexive. By adding and to , is now reflexive. This new relation contains . Any reflexive relation that contains must also contain and . Because this relation contains , is reflexive, and is contained within every reflexive relation that contains , it is called the reflexive closure of .
As the above example illustrates, given a relation on a set , the reflexive closure of can be formed by adding to all pairs of the form with , not already in . The addition of these pairs produces a new relation that is reflexive, contains , and is contained within any reflexive relation containing .
We see that the reflexive closure of equals , where is the diagonal relation on .
¶ Example
What is the reflexive closure of the relation on the set of integers?
The reflexive closure of is
¶ Symmetric Closure
The relation on a set can be made symmetric by adding and , the only pairs of the form with that are not in . This new relation is the symmetric closure of .
The symmetric closure of a relation can be constructed by taking the union of a relation with its inverse, this is, is the symmetric closure of , where .
¶ Example
What is the symmetric closure of the relation on the set of positive integers?
¶ Transitive Closures
These are a little more complicated. Take for example a relation on a set . The relation isn't transitive because it does not contain all pairs of the form where and are in . The pairs of this form not in are , , , and . Adding these pairs doesn't produce a transitive relation because the resulting relation contains and but does not contain .
¶ Paths in Directed Graphs
A path from to in the directed graph is a sequence of edges , in , where is a nonnegative integer, and and , that is, a sequence of edges where the terminal vertex of an edge is the same as the initial vertex in the next edge in the path. This path is denoted by and has length . We view the empty set of edges as a path of length zero from to . A path of length that begins and ends at the same vertex is called a circuit or cycle.
The term path also applies to relations. Carrying over the definition from directed graphs to relations, there is a path from to in if there is a sequence of elements with , and Theorem 1 can be obtained from the definition of a path in a relation.
¶ Theorem 1
Let be a relation on a set . There is a path of length , where is a positive integer, from to if and only if .
¶ Proof of Theorem 1
Proof: We will use mathematical induction. By definition, there is a path from to of length one if and only if , so the theorem is true when .
Assume that the theorem is true for the positive integer . This is the inductive hypothesis. There is a path of length from to if and only if there is an element such that there is a path of length one from to , so , and a path of length from to , that is, Consequently, by the inductive hypothesis, there is a path of length from to if and only if there is an element with and But there is such an element if and only if . Therefore, there is a path of length from to if and only if . This completes the proof.
¶ Transitive Closures and Connectivity Relation
Transitive closures of a relation are equivalent to determining which pairs of vertices in the associated digraph are connected by a path. With this in mind, we define a new relation.
Let be a relation on a set The connectivity relation consists of the pairs such that there is a path of length at least one from to in .
Because consists of the pairs such that there is a path of length from to , it follows that is the union of all the sets In other words,
¶ Example
Let be the relation on the set of all people in the world that contains if has met . What is , where is a positive integer greater than one? What is ?
¶ Solution
The relation contains if there is a person such that and that is, if there is a person such that has met and has met . Similarly, consists of those pairs such that there are people such that has met has met , and has met .
The relation contains if there is a sequence of people, starting with and ending with , such that each person in the sequence has met the next person in the sequence.
¶ Example
Let be the relation on the set of all subway stops in New York City that contains if it is possible to travel from stop to stop without changing trains. What is when is a positive integer? What is ?
¶ Solution
The relation contains if it is possible to travel from stop to stop by making at most changes of trains. The relation consists of the ordered pairs where it is possible to travel from stop to stop making as many changes of trains as necessary.
¶ Theorem 2
The transitive closure of a relation equals the connectivity relation .
¶ Proof of Theorem 2
Note that contains by definition. To show that is the transitive closure of we must also show that is transitive and that whenever is a transitive relation that contains .
First, we show that is transitive. If and , then there are paths from to and from to in . We obtain a path from to by starting with the path from to and following it with the path from to . Hence, . It follows that is transitive. Now suppose that is a transitive relation containing . Because is transitive, also is transitive and . Furthermore, because
and , it follows that Now note that if , then , because any path in is also a path in Consequently, Thus, any transitive relation that contains must also contain . Therefore, is the transitive closure of .
¶ Lemma 1
This lemma shows it is sufficient to examine paths containing no more than edges, where is the number of elements in the set.
Let be a set with elements, and let be a relation on . If there is a path of length at least one in from to , then there is such a path with length not exceeding . Moreover, when , if there is a path of length at least one in from to , then there is such a path with length not exceeding .
¶ Proof of Lemma 1
Proof: Suppose there is a path from to in . Let be the length of the shortest such path. Suppose that , where and , is such a path.
Suppose that and that , so that By the pigeonhole principle, because there are vertices in , among the vertices , at least two are equal (see below digraph)
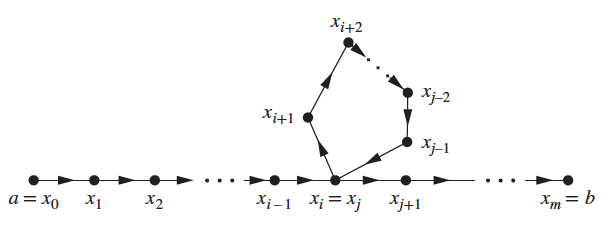
Suppose that with . Then the path contains a circuit from to itself. This circuit can be deleted from the path from to , leaving a path, namely, , from to of shorter length. Hence, the path of shortest length must have length less than or equal to .
¶ Theorem 3
Let be the zero-one matrix of the relation on a set with elements. Then the zero-one matrix of the transitive closure is
¶ Example
Find the zero-one matrix of the transitive closure of the relation where
¶ Solution
Solution: By Theorem 3, it follows that the zero-one matrix of is
Because
it follows that